Ice Ih: Difference between revisions

From SklogWiki
Jump to navigation Jump to search
m (→‎Melting point: Finished fixing references.)
m (→‎Melting point: Added data)
 
(23 intermediate revisions by 2 users not shown)
Line 1: Line 1:
'''Ice Ih''' (hexagonal ice) is a proton disordered [[Ice phases |ice phase]] having the space group P6<sub>3</sub>/mmc. Ice Ih has the following lattice parameters at 250 K:  ''a''=4.51842 &Aring;, <math>b=a\sqrt3</math>, and ''c''=7.35556 &Aring; with four molecules per  unit cell  
[[Image:Ice_Ih.png|thumb|right]]
'''Ice Ih''', also known as hexagonal ice, is a proton disordered [[Ice phases |ice phase]] having the space group P6<sub>3</sub>/mmc. Ice Ih has the following lattice parameters at 250 K:  ''a''=4.51842 &Aring;, <math>b=a\sqrt3</math>, and ''c''=7.35556 &Aring; with four molecules per  unit cell  
(in Table 3 of <ref>[http://dx.doi.org/10.1107/S0108768194004933 K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. F. Kuhs "Lattice constants and thermal expansion of H2O and D2O ice Ih between 10 and 265 K", Acta Crystallographica Section B '''50''' pp. 644-648 (1994)]</ref>).  
(in Table 3 of <ref>[http://dx.doi.org/10.1107/S0108768194004933 K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. F. Kuhs "Lattice constants and thermal expansion of H2O and D2O ice Ih between 10 and 265 K", Acta Crystallographica Section B '''50''' pp. 644-648 (1994)]</ref>).  
The proton ordered form of ice Ih is known as [[ice XI]], which (in principle) forms when ice Ih is cooled to below 72K (it is usually doped with KOH to aid the transition).
The proton ordered form of ice Ih is known as [[ice XI]], which (in principle) forms when ice Ih is cooled to below 72K (it is usually doped with KOH to aid the transition).
==Melting point==
==Melting point==
The following is a collection of melting points <math>(T_m)</math> for the ice Ih-[[water]] transition:
The following is a collection of melting points <math>(T_m)</math> for the ice Ih-[[water]] transition (in ascending order):
:{| border="1"
:{| border="1"
|-  
|-  
| <math>T_m</math> || Pressure || [[Water models|Water model]]/technique  || Reference
| <math>T_m</math> || Pressure || [[Water models|Water model]] / technique  || Reference
|-   
|-   
|<math>146~K</math> || 1 bar || [[TIP3P]]  || <ref name="multiple3"> [http://dx.doi.org/10.1039/b805531a C. Vega, J. L. F. Abascal, M. M. Conde and J. L. Aragones "What ice can teach us about water interactions: a critical comparison of the performance of different water models", Faraday Discussions '''141''' pp. 251-276 (2009)] </ref>
|<math>146~K</math> || 1 bar || [[TIP3P]]  || <ref name="multiple3"> [http://dx.doi.org/10.1039/b805531a C. Vega, J. L. F. Abascal, M. M. Conde and J. L. Aragones "What ice can teach us about water interactions: a critical comparison of the performance of different water models", Faraday Discussions '''141''' pp. 251-276 (2009)] </ref>
|- 
|<math>149~K</math> || 1 bar || [[COS model of water |COS/G3]]  || <ref name="KBB_194102">[http://dx.doi.org/10.1063/1.4767063  Péter T. Kiss, Péter Bertsyk, and András Baranyai "Testing recent charge-on-spring type polarizable water models. I. Melting temperature and ice properties", Journal of Chemical Physics '''137''' 194102 (2012)]</ref>
|- 
|<math>180~K \pm 10~K </math> || 1 bar || [[POL3]]  || <ref>[http://dx.doi.org/10.1021/jp110391q Eva Muchová, Ivan Gladich, Sylvain Picaud, Paul N. M. Hoang, and Martina Roeselová "The Ice−Vapor Interface and the Melting Point of Ice Ih for the Polarizable POL3 Water Model", Journal of Physical Chemistry A  '''115''' pp. 5973-5982 (2011)]</ref>
|- 
|<math>186~K</math> || 1 bar || [[SWM4-DP model of water | SWM4-DP]]  || <ref name="KBB_194102"> </ref>
|-   
|-   
|<math>190~K</math> || 1 bar || [[SPC]]  || <ref name="multiple3">  </ref>
|<math>190~K</math> || 1 bar || [[SPC]]  || <ref name="multiple3">  </ref>
|- 
|<math>207~K</math> || 1 bar || [[BK water models | BKd1]]  || <ref name="KBB_194102"> </ref>
|- 
|<math>213~K</math> || 1 bar || [[BK water models | BKd2]]  || <ref name="KBB_194102"> </ref>
|- 
|<math>215~K</math> || 1 bar || [[COS model of water |COS/G2]]  || <ref name="KBB_194102"> </ref>
|-
|-
|<math>215(4)~K</math> || 1 bar || [[SPC/E]] / [[Computation of phase equilibria | free energy calculation]] || <ref name="multiple1"> [http://dx.doi.org/10.1080/00268970600967948  Carlos Vega, Maria Martin-Conde and Andrzej Patrykiejew "Absence of superheating for ice Ih with a free surface: a new method of determining the melting point of different water models", Molecular Physics '''104''' pp. 3583-3592 (2006)]</ref>
|<math>215(4)~K</math> || 1 bar || [[SPC/E]] / [[Computation of phase equilibria | free energy calculation]] || <ref name="multiple1"> [http://dx.doi.org/10.1080/00268970600967948  Carlos Vega, Maria Martin-Conde and Andrzej Patrykiejew "Absence of superheating for ice Ih with a free surface: a new method of determining the melting point of different water models", Molecular Physics '''104''' pp. 3583-3592 (2006)]</ref>
|-
|<math>225~K</math> || 1 bar || [[TTM3-F model of water |TTM3-F]] ([[Path integral formulation |quantum]]) || <ref>[http://dx.doi.org/10.1021/jz100734w Francesco Paesani, Soohaeng Yoo, Huib J. Bakker and Sotiris S. Xantheas "Nuclear Quantum Effects in the Reorientation of Water",Journal of Physical Chemistry Letters  '''1''' pp. 2316-2321 (2010)]</ref>
|-  
|-  
| <math>227.65 \pm 1.5~K</math> || 1 bar || [[TTM2.1-F]] ([[Path integral formulation |quantum]]) || <ref name="multiple4"> [http://dx.doi.org/10.1021/jp710640e Francesco Paesani and Gregory A. Voth "Quantum Effects Strongly Influence the Surface Premelting of Ice", Journal of Physical Chemistry C '''112''' pp. 324-327 (2008)]</ref>
| <math>227.65 \pm 1.5~K</math> || 1 bar || [[TTM2.1-F]] ([[Path integral formulation |quantum]]) || <ref name="multiple4"> [http://dx.doi.org/10.1021/jp710640e Francesco Paesani and Gregory A. Voth "Quantum Effects Strongly Influence the Surface Premelting of Ice", Journal of Physical Chemistry C '''112''' pp. 324-327 (2008)]</ref>
|-
|-
|<math>232(4)~K</math> || 1 bar ||[[TIP4P]] / [[Computation of phase equilibria | free energy calculation]] || <ref name="multiple1"> </ref>
|<math>232(4)~K</math> || 1 bar ||[[TIP4P]] / [[Computation of phase equilibria | free energy calculation]] || <ref name="multiple1"> </ref>
|- 
|<math>233~K</math> || 1 bar || [[BK water models | BKd3]]  || <ref name="KBB_194102"> </ref>
|-  
|-  
| <math>242.65 \pm 1.5~K</math> || 1 bar || [[TTM2.1-F]] (classical) || <ref name="multiple4" > </ref>
| <math>242.65 \pm 1.5~K</math> || 1 bar || [[TTM2.1-F]] (classical) || <ref name="multiple4" > </ref>
|-
|-
|<math>245.5(6)~K</math> || 1 bar || [[TIP4P/Ew]] / [[Computation of phase equilibria | free energy calculation]] || <ref name="multiple1"> </ref>
|<math>245.5(6)~K</math> || 1 bar || [[TIP4P/Ew]] / [[Computation of phase equilibria | free energy calculation]] || <ref name="multiple1"> </ref>
|-
|<math>248~K</math> || 1 bar || [[TTM3-F]]  || <ref name="Yoo">[http://dx.doi.org/10.1063/1.3573375 Soohaeng Yoo and Sotiris S. Xantheas  "Communication: The effect of dispersion corrections on the melting temperature of liquid water", Journal of Chemical Physics '''134''' 121105 (2011)]</ref>
|-
| <math>251 \pm 1~K </math>  ||  1 bar || [[Q-TIP4P/F model of water | q-TIP4P/F ]] / [[Computation of phase equilibria#Direct simulation of the two phase system | direct coexistence]]|| <ref>[http://dx.doi.org/10.1063/1.3167790 Scott Habershon, Thomas E. Markland, and David E. Manolopoulos "Competing quantum effects in the dynamics of a flexible water model", Journal of Chemical Physics '''131''' 024501 (2009)]</ref>
|-
|-
| <math>252(6)~K</math>  ||  1 bar || [[TIP4P/2005]] / [[Computation of phase equilibria | free energy calculation]] || <ref name="multiple1"> </ref>
| <math>252(6)~K</math>  ||  1 bar || [[TIP4P/2005]] / [[Computation of phase equilibria | free energy calculation]] || <ref name="multiple1"> </ref>
Line 29: Line 50:
|-   
|-   
|<math>274~K</math> || 1 bar || [[TIP5P]]  || <ref name="multiple3">  </ref>
|<math>274~K</math> || 1 bar || [[TIP5P]]  || <ref name="multiple3">  </ref>
|- 
|<math>274.6~K</math> || 1 bar || [[MW model of water | mW]]  || <ref>[http://dx.doi.org/10.1021/jp805227c Valeria Molinero and Emily B. Moore "Water Modeled As an Intermediate Element between Carbon and Silicon", Journal of Physical Chemistry B '''113''' pp. 4008-4016 (2009)]</ref>
|-   
|-   
|<math>289~K</math> || 1 bar || [[NvdE]]  || <ref>[http://dx.doi.org/10.1063/1.2360276    José L. F. Abascal, Ramón García Fernández, Carlos Vega and  Marcelo A. Carignano, "The melting temperature of the six site potential model of water", Journal of Chemical Physics, '''125''' 166101 (2006)]</ref>
|<math>289~K</math> || 1 bar || [[NvdE]]  || <ref>[http://dx.doi.org/10.1063/1.2360276    José L. F. Abascal, Ramón García Fernández, Carlos Vega and  Marcelo A. Carignano, "The melting temperature of the six site potential model of water", Journal of Chemical Physics, '''125''' 166101 (2006)]</ref>
|-
|-
| <math>411 \pm 4~K</math>  ||10,000 bar ||  [[Becke-Lee-Yang-Parr functional]] ||  <ref name="multiple2"> [http://dx.doi.org/10.1063/1.3153871 Soohaeng Yoo, Xiao Cheng Zeng, and Sotiris S. Xantheas "On the phase diagram of water with density functional theory potentials: The melting temperature of ice Ih with the Perdew–Burke–Ernzerhof and Becke–Lee–Yang–Parr functionals", Journal of Chemical Physics '''130''' 221102 (2009)] </ref>
|  <math>303\pm 8~K</math>  || 1 bar ||  [[TIP4P/FQ model of water | TIP4P/FQ]]  ||  <ref>[http://dx.doi.org/10.1016/j.jcrysgro.2006.04.077  Benjamin F. Nicholson, Paulette Clancy and Steven W. Rick "The interface response function and melting point of the prism interface of ice Ih using a fluctuating charge model (TIP4P-FQ)", Journal of Crystal Growth '''293''' pp. 78-85 (2006)]</ref>
|-
|<math>360~K</math> || 1 bar ||  [[Becke-Lee-Yang-Parr functional | BLYP-D]] || <ref name="Yoo"> </ref>
|-
| <math>411 \pm 4~K</math>  ||10,000 bar ||  [[Becke-Lee-Yang-Parr functional |BLYP]] ||  <ref name="multiple2"> [http://dx.doi.org/10.1063/1.3153871 Soohaeng Yoo, Xiao Cheng Zeng, and Sotiris S. Xantheas "On the phase diagram of water with density functional theory potentials: The melting temperature of ice Ih with the Perdew–Burke–Ernzerhof and Becke–Lee–Yang–Parr functionals", Journal of Chemical Physics '''130''' 221102 (2009)] </ref>
|-
|-
|  <math>417\pm 3~K</math>  || 2500 bar ||  [[Perdew-Burke-Ernzerhof functional]] ||  <ref name="multiple2" > </ref>
|  <math>417\pm 3~K</math>  || 2500 bar ||  [[Perdew-Burke-Ernzerhof functional]] ||  <ref name="multiple2" > </ref>
|}
|}
'''Related reading'''
'''Isotopes:'''
:{| border="1"
|-
| <math>T_m</math> (D<sub>2</sub>0) || Pressure || [[Water models|Water model]] / technique  || Reference
|- 
|<math>257.5(5)~K</math> || 1 bar || [[Q-TIP4P/F model of water | q-TIP4P/F ]] / [[Computation of phase equilibria | free energy calculation]]  ||  <ref name="Ramirez1"> [http://dx.doi.org/10.1063/1.3503764  R. Ramírez  and C. P. Herrero  "Quantum path integral simulation of isotope effects in the melting temperature of ice Ih", Journal of Chemical Physics 133, 144511 (2010)]</ref>
|- 
|<math>263.2~K</math> || 1 bar || [[TIP4PQ_D2O model of water | TIP4PQ_D2O]] / [[Computation of phase equilibria | free energy calculation]]  ||  <ref name="McBride_1">http://dx.doi.org/10.1039/C2CP42393F Carl McBride ,  Juan L. Aragones ,  Eva G. Noya and Carlos Vega "A study of the influence of isotopic substitution on the melting point and temperature of maximum density of water by means of path integral simulations of rigid models", PCCP '''14''' pp. 15199-15205 (2012)]</ref>
|-
| <math>276.83 \pm 0.02 K</math> || 1 bar || <FONT COLOR="#9400D3">experimental value</FONT> || <ref>[http://dx.doi.org/10.1016/j.jct.2005.09.005  N.N. Smirnova, T.A. Bykova, K. Van Durme and B. Van Mele "Thermodynamic properties of deuterium oxide in the temperature range from 6 to 350 K", The Journal of Chemical Thermodynamics '''38''' pp. 879-883 (2006)]</ref>
|}
 
:{| border="1"
|-
| <math>T_m</math> (T<sub>2</sub>0) || Pressure || [[Water models|Water model]] / technique  || Reference
|- 
|<math>259.2(5)~K</math> || 1 bar || [[Q-TIP4P/F model of water | q-TIP4P/F ]] / [[Computation of phase equilibria | free energy calculation]]  ||  <ref name="Ramirez1"> </ref>
|- 
|<math>263.5~K</math> || 1 bar || [[TIP4PQ_T2O model of water | TIP4PQ_T2O]] / [[Computation of phase equilibria | free energy calculation]]  ||  <ref name="McBride_1"> </ref>
|-
| <math>277.64  K</math> || 0.6629 kPa || <FONT COLOR="#9400D3">experimental value</FONT> || <ref>[http://dx.doi.org/10.1063/1.1565352 H. W. Xiang "Vapor Pressure and Critical Point of Tritium Oxide", Journal of Physical and Chemical Reference Data '''32''' pp. 1707.1711 (2003)]</ref>
|}
It is worth pointing out that the calculations presented in the work of Ramírez and  Herrero <ref name="Ramirez1"> </ref> used the melting point of the [[Q-TIP4P/F model of water | q-TIP4P/F model]] as its "reference state". It is perhaps more fruitful to examine the relative changes upon isotopic substitution: <math>\Delta T_m (D_2O - H_2 0) = 6.5 K</math> (experimental value: 3.68 K) and <math>\Delta T_m (T_2O - H_2 0) = 8.2 K</math> (experimental value: 4.49 K).
<br/>'''Related reading'''


*[http://dx.doi.org/10.1039/b703873a Jose L. F. Abascal and C. Vega "The melting point of hexagonal ice (Ih) is strongly dependent on the quadrupole of the water models", PCCP '''9''' pp. 2775 - 2778 (2007)]
*[http://dx.doi.org/10.1039/b703873a Jose L. F. Abascal and C. Vega "The melting point of hexagonal ice (Ih) is strongly dependent on the quadrupole of the water models", PCCP '''9''' pp. 2775 - 2778 (2007)]


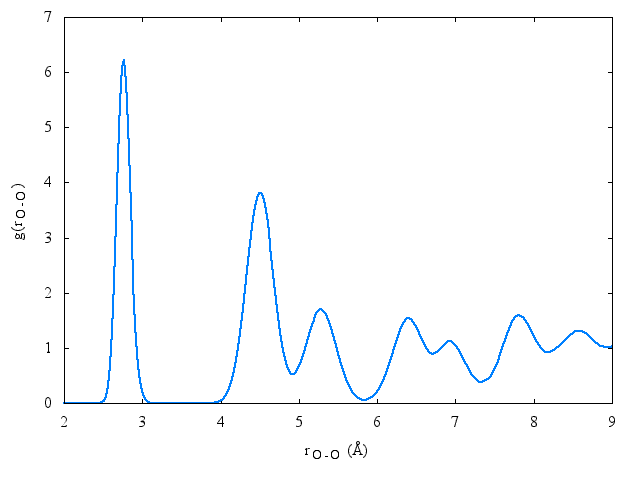
==Radial distribution function==
==Radial distribution function==
The following is a plot of the oxygen-oxygen [[radial distribution function]] for the [[TIP4PQ/2005]] model at 77K
:[[Image:rdf_Ih_OO_77K_TIP4PQ2005.png]]
'''Related reading'''
*[http://dx.doi.org/10.1039/b418934e Carlos Vega, Carl McBride, Eduardo Sanz and Jose L. F. Abascal "Radial distribution functions and densities for the SPC/E, TIP4P and TIP5P models for liquid water and ices Ih, Ic, II, III, IV, V, VI, VII, VIII, IX, XI and XII", Physical Chemistry Chemical Physics '''7''' pp. 1450 - 1456 (2005)]
*[http://dx.doi.org/10.1039/b418934e Carlos Vega, Carl McBride, Eduardo Sanz and Jose L. F. Abascal "Radial distribution functions and densities for the SPC/E, TIP4P and TIP5P models for liquid water and ices Ih, Ic, II, III, IV, V, VI, VII, VIII, IX, XI and XII", Physical Chemistry Chemical Physics '''7''' pp. 1450 - 1456 (2005)]
==Phonon density of states==
==Phonon density of states==
In
In
<ref>[http://dx.doi.org/10.1016/S0921-4526(99)01699-3  Shunle Dong and Jichen Li "The test of water potentials by simulating the vibrational dynamics of ice", Physica B '''276-278''' pp. 469-470 (2000)  ]</ref>
<ref>[http://dx.doi.org/10.1016/S0921-4526(99)01699-3  Shunle Dong and Jichen Li "The test of water potentials by simulating the vibrational dynamics of ice", Physica B '''276-278''' pp. 469-470 (2000)  ]</ref>
the phonon density of states for the [[POL1]], [[TIPS2]], [[TIP4P]], [[TIP3P]], [[SPC]], [[R|Rowlinson]], [[MCY]], and [[BF]] [[water models | models for water]] are compared to experiment.
the phonon density of states for the [[POL1]], [[TIPS2]], [[TIP4P]], [[TIP3P]], [[SPC]], [[R|Rowlinson]], [[MCY]], and [[BF]] [[water models | models for water]] are compared to experiment.
 
==Entropy==
:''Main article: [[Entropy of ice phases]]''
*[http://dx.doi.org/10.1021/ja01315a102 Linus Pauling "The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement", Journal of the American Chemical Society '''57''' pp. 2674 - 2680 (1935)]
==Experimental data==
==Experimental data==
*[http://dx.doi.org/10.1063/1.2183324  Rainer Feistel and Wolfgang Wagner "A New Equation of State for H2O Ice Ih", Journal of Physical and Chemical Reference Data '''35''' pp. 1021- (2006)]
*[http://dx.doi.org/10.1063/1.2183324  Rainer Feistel and Wolfgang Wagner "A New Equation of State for H2O Ice Ih", Journal of Physical and Chemical Reference Data '''35''' pp. 1021- (2006)]
Line 52: Line 108:
<references/>
<references/>
'''Related reading'''
'''Related reading'''
*[http://dx.doi.org/10.1021/ja01315a102 Linus Pauling "The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement", Journal of the American Chemical Society '''57''' pp. 2674 - 2680 (1935)]
*[http://dx.doi.org/10.1021/jp0743121 E. G. Noya, C. Menduiña, J. L. Aragones, and C. Vega "Equation of State, Thermal Expansion Coefficient, and Isothermal Compressibility for Ices Ih, II, III, V, and VI, as Obtained from Computer Simulation", Journal of Physical Chemistry C '''111''' pp. 15877 - 15888 (2007)]
*[http://dx.doi.org/10.1021/jp0743121 E. G. Noya, C. Menduiña, J. L. Aragones, and C. Vega "Equation of State, Thermal Expansion Coefficient, and Isothermal Compressibility for Ices Ih, II, III, V, and VI, as Obtained from Computer Simulation", Journal of Physical Chemistry C '''111''' pp. 15877 - 15888 (2007)]
*[http://dx.doi.org/10.1016/S1293-2558(03)00092-X Sten Andersson and B.W. Ninham "Why ice floats on water", Solid State Sciences '''5''' pp. 683-693 (2003)]
*[http://dx.doi.org/10.1063/1.3507916 Ikutaro Hamada "A van der Waals density functional study of ice Ih", Journal of Chemical Physics '''133''' 214503 (2010)]


==External links==
*[http://www.lsbu.ac.uk/water/ice1h.html Hexagonal Ice (Ice Ih)] page on [http://www.lsbu.ac.uk/water/ Martin Chaplin's Water Structure and Science] web site.
{{numeric}}
{{numeric}}
[[category: water]]
[[category: water]]

Latest revision as of 15:37, 22 November 2012

Ice Ih, also known as hexagonal ice, is a proton disordered ice phase having the space group P63/mmc. Ice Ih has the following lattice parameters at 250 K: a=4.51842 Å, , and c=7.35556 Å with four molecules per unit cell (in Table 3 of [1]). The proton ordered form of ice Ih is known as ice XI, which (in principle) forms when ice Ih is cooled to below 72K (it is usually doped with KOH to aid the transition).

Melting point[edit]

The following is a collection of melting points for the ice Ih-water transition (in ascending order):

Pressure Water model / technique Reference
1 bar TIP3P [2]
1 bar COS/G3 [3]
1 bar POL3 [4]
1 bar SWM4-DP [3]
1 bar SPC [2]
1 bar BKd1 [3]
1 bar BKd2 [3]
1 bar COS/G2 [3]
1 bar SPC/E / free energy calculation [5]
1 bar TTM3-F (quantum) [6]
1 bar TTM2.1-F (quantum) [7]
1 bar TIP4P / free energy calculation [5]
1 bar BKd3 [3]
1 bar TTM2.1-F (classical) [7]
1 bar TIP4P/Ew / free energy calculation [5]
1 bar TTM3-F [8]
1 bar q-TIP4P/F / direct coexistence [9]
1 bar TIP4P/2005 / free energy calculation [5]
1 bar TIP4P/Ice / free energy calculation [5]
1 bar experimental value
1 bar TIP5P [2]
1 bar mW [10]
1 bar NvdE [11]
1 bar TIP4P/FQ [12]
1 bar BLYP-D [8]
10,000 bar BLYP [13]
2500 bar Perdew-Burke-Ernzerhof functional [13]

Isotopes:

(D20) Pressure Water model / technique Reference
1 bar q-TIP4P/F / free energy calculation [14]
1 bar TIP4PQ_D2O / free energy calculation [15]
1 bar experimental value [16]
(T20) Pressure Water model / technique Reference
1 bar q-TIP4P/F / free energy calculation [14]
1 bar TIP4PQ_T2O / free energy calculation [15]
0.6629 kPa experimental value [17]

It is worth pointing out that the calculations presented in the work of Ramírez and Herrero [14] used the melting point of the q-TIP4P/F model as its "reference state". It is perhaps more fruitful to examine the relative changes upon isotopic substitution: (experimental value: 3.68 K) and (experimental value: 4.49 K).
Related reading

Radial distribution function[edit]

The following is a plot of the oxygen-oxygen radial distribution function for the TIP4PQ/2005 model at 77K

Related reading

Phonon density of states[edit]

In [18] the phonon density of states for the POL1, TIPS2, TIP4P, TIP3P, SPC, Rowlinson, MCY, and BF models for water are compared to experiment.

Entropy[edit]

Main article: Entropy of ice phases

Experimental data[edit]

References[edit]

  1. ↑ K. Röttger, A. Endriss, J. Ihringer, S. Doyle and W. F. Kuhs "Lattice constants and thermal expansion of H2O and D2O ice Ih between 10 and 265 K", Acta Crystallographica Section B 50 pp. 644-648 (1994)
  2. ↑ 2.0 2.1 2.2 C. Vega, J. L. F. Abascal, M. M. Conde and J. L. Aragones "What ice can teach us about water interactions: a critical comparison of the performance of different water models", Faraday Discussions 141 pp. 251-276 (2009)
  3. ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Péter T. Kiss, Péter Bertsyk, and András Baranyai "Testing recent charge-on-spring type polarizable water models. I. Melting temperature and ice properties", Journal of Chemical Physics 137 194102 (2012)
  4. ↑ Eva Muchová, Ivan Gladich, Sylvain Picaud, Paul N. M. Hoang, and Martina Roeselová "The Ice−Vapor Interface and the Melting Point of Ice Ih for the Polarizable POL3 Water Model", Journal of Physical Chemistry A 115 pp. 5973-5982 (2011)
  5. ↑ 5.0 5.1 5.2 5.3 5.4 Carlos Vega, Maria Martin-Conde and Andrzej Patrykiejew "Absence of superheating for ice Ih with a free surface: a new method of determining the melting point of different water models", Molecular Physics 104 pp. 3583-3592 (2006)
  6. ↑ Francesco Paesani, Soohaeng Yoo, Huib J. Bakker and Sotiris S. Xantheas "Nuclear Quantum Effects in the Reorientation of Water",Journal of Physical Chemistry Letters 1 pp. 2316-2321 (2010)
  7. ↑ 7.0 7.1 Francesco Paesani and Gregory A. Voth "Quantum Effects Strongly Influence the Surface Premelting of Ice", Journal of Physical Chemistry C 112 pp. 324-327 (2008)
  8. ↑ 8.0 8.1 Soohaeng Yoo and Sotiris S. Xantheas "Communication: The effect of dispersion corrections on the melting temperature of liquid water", Journal of Chemical Physics 134 121105 (2011)
  9. ↑ Scott Habershon, Thomas E. Markland, and David E. Manolopoulos "Competing quantum effects in the dynamics of a flexible water model", Journal of Chemical Physics 131 024501 (2009)
  10. ↑ Valeria Molinero and Emily B. Moore "Water Modeled As an Intermediate Element between Carbon and Silicon", Journal of Physical Chemistry B 113 pp. 4008-4016 (2009)
  11. ↑ José L. F. Abascal, Ramón García Fernández, Carlos Vega and Marcelo A. Carignano, "The melting temperature of the six site potential model of water", Journal of Chemical Physics, 125 166101 (2006)
  12. ↑ Benjamin F. Nicholson, Paulette Clancy and Steven W. Rick "The interface response function and melting point of the prism interface of ice Ih using a fluctuating charge model (TIP4P-FQ)", Journal of Crystal Growth 293 pp. 78-85 (2006)
  13. ↑ 13.0 13.1 Soohaeng Yoo, Xiao Cheng Zeng, and Sotiris S. Xantheas "On the phase diagram of water with density functional theory potentials: The melting temperature of ice Ih with the Perdew–Burke–Ernzerhof and Becke–Lee–Yang–Parr functionals", Journal of Chemical Physics 130 221102 (2009)
  14. ↑ 14.0 14.1 14.2 R. Ramírez and C. P. Herrero "Quantum path integral simulation of isotope effects in the melting temperature of ice Ih", Journal of Chemical Physics 133, 144511 (2010)
  15. ↑ 15.0 15.1 http://dx.doi.org/10.1039/C2CP42393F Carl McBride , Juan L. Aragones , Eva G. Noya and Carlos Vega "A study of the influence of isotopic substitution on the melting point and temperature of maximum density of water by means of path integral simulations of rigid models", PCCP 14 pp. 15199-15205 (2012)]
  16. ↑ N.N. Smirnova, T.A. Bykova, K. Van Durme and B. Van Mele "Thermodynamic properties of deuterium oxide in the temperature range from 6 to 350 K", The Journal of Chemical Thermodynamics 38 pp. 879-883 (2006)
  17. ↑ H. W. Xiang "Vapor Pressure and Critical Point of Tritium Oxide", Journal of Physical and Chemical Reference Data 32 pp. 1707.1711 (2003)
  18. ↑ Shunle Dong and Jichen Li "The test of water potentials by simulating the vibrational dynamics of ice", Physica B 276-278 pp. 469-470 (2000)

Related reading

External links[edit]

This page contains numerical values and/or equations. If you intend to use ANY of the numbers or equations found in SklogWiki in any way, you MUST take them from the original published article or book, and cite the relevant source accordingly.
Retrieved from "http://www.sklogwiki.org/SklogWiki/index.php?title=Ice_Ih&oldid=13212"