Ice Ih

Ice Ih, also known as hexagonal ice, is a proton disordered ice phase having the space group P6₃/mmc. Ice Ih has the following lattice parameters at 250 K: a=4.51842 Å, $b=a{\sqrt {3}}$, and c=7.35556 Å with four molecules per unit cell (in Table 3 of ). The proton ordered form of ice Ih is known as ice XI, which (in principle) forms when ice Ih is cooled to below 72K (it is usually doped with KOH to aid the transition).

Melting point

The following is a collection of melting points $(T_{m})$ for the ice Ih-water transition:

$T_{m}$	Pressure	Water model / technique	Reference
$146~K$	1 bar	TIP3P
$190~K$	1 bar	SPC
$215(4)~K$	1 bar	SPC/E / free energy calculation
$225~K$	1 bar	TTM3-F (quantum)
$227.65\pm 1.5~K$	1 bar	TTM2.1-F (quantum)
$232(4)~K$	1 bar	TIP4P / free energy calculation
$242.65\pm 1.5~K$	1 bar	TTM2.1-F (classical)
$245.5(6)~K$	1 bar	TIP4P/Ew / free energy calculation
$251\pm 1~K$	1 bar	q-TIP4P/F / direct coexistence
$252(6)~K$	1 bar	TIP4P/2005 / free energy calculation
$272(6)~K$	1 bar	TIP4P/Ice / free energy calculation
$273.15K$	1 bar	experimental value
$274~K$	1 bar	TIP5P
$289~K$	1 bar	NvdE
$411\pm 4~K$	10,000 bar	Becke-Lee-Yang-Parr functional
$417\pm 3~K$	2500 bar	Perdew-Burke-Ernzerhof functional

Isotopes:

$T_{m}$ (D20)	Pressure	Water model / technique	Reference
$257.5(5)~K$	1 bar	q-TIP4P/F / free energy calculation
$276.83\pm 0.02K$	1 bar	experimental value

$T_{m}$ (T20)	Pressure	Water model / technique	Reference
$259.2(5)~K$	1 bar	q-TIP4P/F / free energy calculation
$277.64K$	0.6629 kPa	experimental value

It is worth pointing out that the calculations presented in the work of Ramírez and Herrero used the melting point of the q-TIP4P/F model as its "reference state". It is perhaps more fruitful to examine the relative changes upon isotopic substitution: $\Delta T_{m}(D_{2}O-H_{2}0)=6.5K$ (experimental value: 3.68 K) and $\Delta T_{m}(T_{2}O-H_{2}0)=8.2K$ (experimental value: 4.49 K).
Related reading

• Jose L. F. Abascal and C. Vega "The melting point of hexagonal ice (Ih) is strongly dependent on the quadrupole of the water models", PCCP 9 pp. 2775 - 2778 (2007)

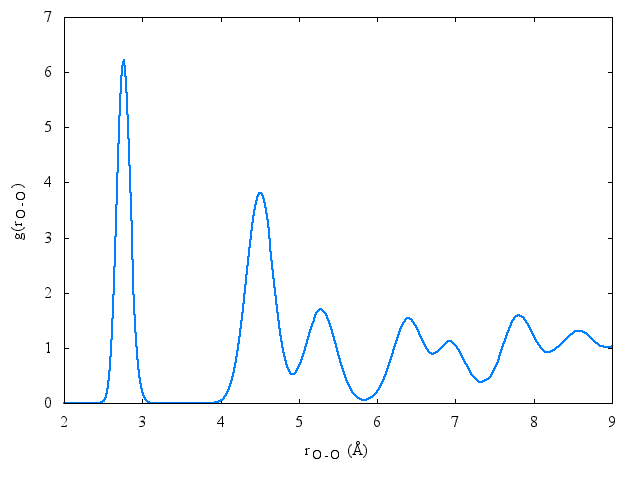
Radial distribution function

The following is a plot of the oxygen-oxygen radial distribution function for the TIP4PQ/2005 model at 77K

Related reading

• Carlos Vega, Carl McBride, Eduardo Sanz and Jose L. F. Abascal "Radial distribution functions and densities for the SPC/E, TIP4P and TIP5P models for liquid water and ices Ih, Ic, II, III, IV, V, VI, VII, VIII, IX, XI and XII", Physical Chemistry Chemical Physics 7 pp. 1450 - 1456 (2005)

Phonon density of states

In the phonon density of states for the POL1, TIPS2, TIP4P, TIP3P, SPC, Rowlinson, MCY, and BF models for water are compared to experiment.

Entropy

Main article: Entropy of ice phases

• Linus Pauling "The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement", Journal of the American Chemical Society 57 pp. 2674 - 2680 (1935)

Experimental data

• Rainer Feistel and Wolfgang Wagner "A New Equation of State for H2O Ice Ih", Journal of Physical and Chemical Reference Data 35 pp. 1021- (2006)

References

Related reading

• E. G. Noya, C. Menduiña, J. L. Aragones, and C. Vega "Equation of State, Thermal Expansion Coefficient, and Isothermal Compressibility for Ices Ih, II, III, V, and VI, as Obtained from Computer Simulation", Journal of Physical Chemistry C 111 pp. 15877 - 15888 (2007)
• Sten Andersson and B.W. Ninham "Why ice floats on water", Solid State Sciences 5 pp. 683-693 (2003)
• Ikutaro Hamada "A van der Waals density functional study of ice Ih", Journal of Chemical Physics 133 214503 (2010)

External links

• Hexagonal Ice (Ice Ih) page on Martin Chaplin's Water Structure and Science web site.