Anisotropic particles with tetrahedral symmetry: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 7: | Line 7: | ||
to the diamond crystal when the range of the interaction becomes short (roughly less than 15% of the | to the diamond crystal when the range of the interaction becomes short (roughly less than 15% of the | ||
diameter). | diameter). | ||
:[[Image:romanojpcb09.gif]] | |||
===Crystallization=== | |||
<ref>[http://dx.doi.org/10.1063/1.3578182 Flavio Romano, Eduardo Sanz, and Francesco Sciortino "Crystallization of tetrahedral patchy particles in silico", Journal of Chemical Physics 134, 174502 (2011)]</ref> | |||
| Line 18: | Line 22: | ||
==Lattice model== | ==Lattice model== | ||
<ref>[http://dx.doi.org/10.1080/00268976.2010.523521 N. G. Almarza and E. G. Noya "Phase transitions of a lattice model for patchy particles with tetrahedral symmetry", Molecular Physics '''109''' pp. 65-74 (2011)]</ref> | <ref>[http://dx.doi.org/10.1080/00268976.2010.523521 N. G. Almarza and E. G. Noya "Phase transitions of a lattice model for patchy particles with tetrahedral symmetry", Molecular Physics '''109''' pp. 65-74 (2011)]</ref> | ||
==See also== | ==See also== | ||
*[[PMW]] (primitive model for [[water]]) | *[[PMW]] (primitive model for [[water]]) | ||
Revision as of 15:09, 8 August 2011
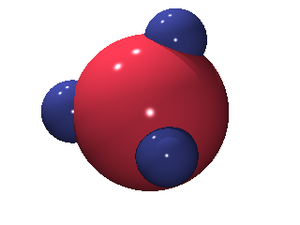
Kern and Frenkel model
Phase diagram
The phase diagram of the tetrahedral Kern and Frenkel patchy model exhibits the following solid phases[1][2]: diamond crystal (DC), body centred cubic (BCC) and face centred cubic (FCC). The gas-liquid critical point becomes metastable with respect to the diamond crystal when the range of the interaction becomes short (roughly less than 15% of the diameter).
Crystallization
In contrast to isotropic models, the critical point becomes only weakly metastable with respect to the solid as the interaction range
narrows (from left to right in the figure).
Modulated patchy Lennard-Jones model
The solid phases of the modulated patchy Lennard-Jones model has also been studied [4]
Lattice model
See also
References
- ↑ Flavio Romano, Eduardo Sanz and Francesco Sciortino "Role of the Range in the Fluid−Crystal Coexistence for a Patchy Particle Model", Journal of Physical Chemistry B 113 pp. 15133–15136 (2009)
- ↑ Flavio Romano, Eduardo Sanz and Francesco Sciortino "Phase diagram of a tetrahedral patchy particle model for different interaction ranges", Journal of Chemical Physics 132 184501 (2010)
- ↑ Flavio Romano, Eduardo Sanz, and Francesco Sciortino "Crystallization of tetrahedral patchy particles in silico", Journal of Chemical Physics 134, 174502 (2011)
- ↑ Eva G. Noya, Carlos Vega, Jonathan P. K. Doye, and Ard A. Louis "The stability of a crystal with diamond structure for patchy particles with tetrahedral symmetry", Journal of Chemical Physics 132 234511 (2010)
- ↑ N. G. Almarza and E. G. Noya "Phase transitions of a lattice model for patchy particles with tetrahedral symmetry", Molecular Physics 109 pp. 65-74 (2011)
- Related reading
