Master equation
|
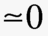
This article is a 'stub' page, it has no, or next to no, content. It is here at the moment to help form part of the structure of SklogWiki. If you add sufficient material to this article then please remove the {{Stub-general}} template from this page. |
The master equation describes the exact behavior of the velocity distribution for any time (Ref. 1 Eq. 3-11)
- Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \partial _{t\rho _{0}}\left(\{{\mathbf {\upsilon } }\},t\right)={\mathcal {D}}_{0}\left(t,\rho _{\{k''\}}\left(\{{\mathbf {\upsilon } }\},0\right)\right)+\int _{0}^{t}G_{00}(t-t')\rho _{0}\left(\{{\upsilon }\},t'\right){\mathrm {d} }t'}
where the time dependent functional of the initial conditions is given by (Ref. 1 Eq. 3-9)
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathcal D}_0 \left(t, \rho_{ \{k'' \} } \left( \{ {\mathbf \upsilon} \},0 \right) \right) = \frac{-1}{2\pi} \oint_c \exp (-izt) \sum_{ \{k'' \} \neq 0} {\mathcal D}^+_{0 \{k'' \}} (z) \rho_{\{k'' \}} \left( \{ {\mathbf \upsilon} \},0 \right) }
and the diagonal fragment is given by (Ref. 1 Eq. 3-10)
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{00}(\tau) = \frac{1}{2\pi i} \oint_c \exp (-iz \tau) \psi^+_{00} (z)~ {\mathrm d}z }