Lennard-Jones model

The Lennard-Jones intermolecular pair potential is a special case of the Mie potential and takes its name from Sir John Edward Lennard-Jones . The Lennard-Jones model consists of two 'parts'; a steep repulsive term, and smoother attractive term, representing the London dispersion forces. Apart from being an important model in its-self, the Lennard-Jones potential frequently forms one of 'building blocks' of may force fields,

Functional form

The Lennard-Jones potential is given by

$\Phi _{12}(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]$

where

• $r:=|\mathbf {r} _{1}-\mathbf {r} _{2}|$
• $\Phi _{12}(r)$ is the intermolecular pair potential between two particles or sites
• $\sigma$ is the diameter (length), i.e. the value of $r$ at which $\Phi _{12}(r)=0$
• $\epsilon$ is the well depth (energy)

In reduced units:

• Density: $\rho ^{*}:=\rho \sigma ^{3}$, where $\rho :=N/V$ (number of particles $N$ divided by the volume $V$)
• Temperature: $T^{*}:=k_{B}T/\epsilon$, where $T$ is the absolute temperature and $k_{B}$ is the Boltzmann constant

The following is a plot of the Lennard-Jones model for the parameters $\epsilon /k_{B}\approx$ 120 K and $\sigma \approx$ 0.34 nm. See argon for different parameter sets.

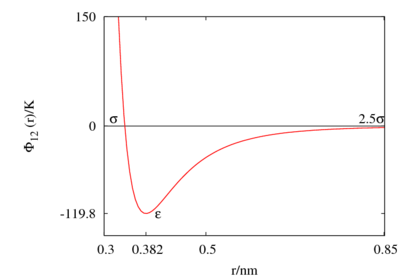
This figure was produced using gnuplot with the command:

plot (4*120*((0.34/x)**12-(0.34/x)**6))

Special points

• $\Phi _{12}(\sigma )=0$
• Minimum value of $\Phi _{12}(r)$ at $r=r_{min}$;

${\frac {r_{min}}{\sigma }}=2^{1/6}\simeq 1.12246...$

Critical point

The location of the critical point is

$T_{c}^{*}=1.326\pm 0.002$

at a reduced density of

$\rho _{c}^{*}=0.316\pm 0.002$.

Vliegenthart and Lekkerkerker have suggested that the critical point is related to the second virial coefficient via the expression

$B_{2}\vert _{T=T_{c}}=-\pi \sigma ^{3}$

Triple point

The location of the triple point as found by Mastny and de Pablo (Ref. 4) is

$T_{tp}^{*}=0.694$

$\rho _{tp}^{*}=0.84$ (liquid); $\rho _{tp}^{*}=0.96$ (solid)

Approximations in simulation: truncation and shifting

The Lennard-Jones model is often used with a cutoff radius of $2.5\sigma$, beyond which $\Phi _{12}(r)$ is set to zero. See Mastny and de Pablo for an analysis of the effect of this cutoff on the melting line.

n-m Lennard-Jones potential

It is relatively common to encounter potential functions given by:

$\Phi _{12}(r)=c_{n,m}\epsilon \left[\left({\frac {\sigma }{r}}\right)^{n}-\left({\frac {\sigma }{r}}\right)^{m}\right].$

with $n$ and $m$ being positive integers and $n>m$. $c_{n,m}$ is chosen such that the minimum value of $\Phi _{12}(r)$ being $\Phi _{min}=-\epsilon$. Such forms are usually referred to as n-m Lennard-Jones Potential. For example, the 9-3 Lennard-Jones interaction potential is often used to model the interaction between the atoms/molecules of a fluid and a continuous solid wall. On the '9-3 Lennard-Jones potential' page a justification of this use is presented. Another example is the n-6 Lennard-Jones potential, where $m$ is fixed at 6, and $n$ is free to adopt a range of integer values. The potentials form part of the larger class of potentials known as the Mie potential.

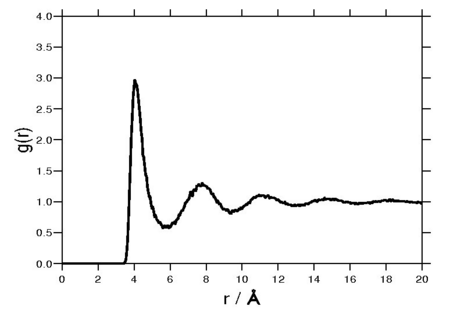
Radial distribution function

The following plot is of a typical radial distribution function for the monatomic Lennard-Jones liquid (here with $\sigma =3.73{\mathrm {\AA} }$ and $\epsilon =0.294$ kcal/mol at a temperature of 111.06K):

Typical radial distribution function for the monatomic Lennard-Jones liquid.

1. John G. Kirkwood, Victor A. Lewinson, and Berni J. Alder "Radial Distribution Functions and the Equation of State of Fluids Composed of Molecules Interacting According to the Lennard-Jones Potential", Journal of Chemical Physics 20 pp. 929- (1952)

Equation of state

Main article: Lennard-Jones equation of state

Virial coefficients

Main article: Lennard-Jones model: virial coefficients

Phase diagram

Main article: Phase diagram of the Lennard-Jones model

Perturbation theory

The Lennard-Jones model is also used in perturbation theories, for example see: Weeks-Chandler-Anderson perturbation theory.

Mixtures

• Binary Lennard-Jones mixtures
• Multicomponent Lennard-Jones mixtures

Related models

• 9-3 Lennard-Jones potential
• 10-4-3 Lennard-Jones potential
• n-6 Lennard-Jones potential
• Kihara potential
• Lennard-Jones model in 1-dimension (rods)
• Lennard-Jones model in 2-dimensions (disks)
• Lennard-Jones model in 4-dimensions
• Lennard-Jones sticks
• Mie potential
• Soft sphere potential
• Stockmayer potential