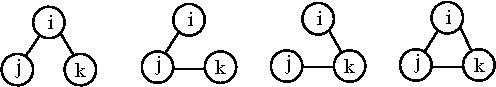Cluster integrals

In an ideal gas there are no intermolecular interactions. However, in an imperfect or real gas, this is not so, and the second virial coefficient is other than zero. Mayer and Mayer developed a theoretical treatment of the virial coefficients in terms of cluster integrals.

The simplest cluster is that consisting of a single molecule, not bound to any other. A cluster of three specified identical molecules, i, j and k may be formed in any of four ways:

The first three cluster integrals are (Eq. 13.6 in )

$b_{1}={\frac {1}{1!V}}\int d\tau _{1}=1$

Ref. 1 Eq. 13.7:

$b_{2}={\frac {1}{2!V}}\iint f(r_{12})d\tau _{2}d\tau _{1}={\frac {1}{2}}\int _{0}^{\infty }4\pi r^{2}f(r)dr$

and Ref. 1 Eq. 13.8:

$b_{3}={\frac {1}{3!V}}\iiint (f_{31}f_{21}+f_{32}f_{31}+f_{32}f_{21}+f_{32}f_{31}f_{21})d\tau _{3}d\tau _{2}d\tau _{1}$

using the Mayer f-function notation.

Irreducible clusters

Irreducible clusters are denoted by $\beta _{k}$

$\beta _{1}=\int f_{31}d\tau _{3}={\frac {1}{V}}\iint f_{12}d\tau _{1}d\tau _{2}=\int _{0}^{\infty }4\pi r^{2}f(r)dr$

note $b_{2}={\frac {1}{2}}\beta _{1}$.

$\beta _{2}={\frac {1}{2V}}\iiint f_{32}f_{31}f_{21}d\tau _{1}d\tau _{2}d\tau _{3}$

note $b_{3}={\frac {1}{2}}\beta _{1}^{2}+{\frac {1}{3}}\beta _{2}$

$\beta _{3}={\frac {1}{6V}}\iiiint (3f_{43}f_{32}f_{21}f_{41}+6f_{43}f_{32}f_{21}f_{41}f_{31}+f_{43}f_{32}f_{21}f_{41}f_{31}f_{42})d\tau _{1}d\tau _{2}d\tau _{3}d\tau _{4}$

note $b_{4}={\frac {2}{3}}\beta _{1}^{3}+\beta _{1}\beta _{2}+{\frac {1}{4}}\beta _{3}$

Hellmann and Bich diagrams

Hellmann and Bich have rederived the virial equation of state from the grand canonical partition function without restricting themselves to pairwise intermolecular pair potentials . This leads to expressions for the virial coefficients that, for $B_{6}$ and beyond, require the evaluation of far fewer diagrams when compared to the original diagrams of Mayer or to the reformulation of Ree and Hoover .

See also

• Cluster diagrams

References

Related reading

• Edwin E. Salpeter "On Mayer's theory of cluster expansions", Annals of Physics 5 pp. 183-223 (1958)