Hard superball model: Difference between revisions
Jump to navigation
Jump to search
(Created page with "thumb|right|The shape of superballs interpolates between octahedra (''q'' = 0.5) and cubes (''q'' = ∞) via spheres (''q'' = 1).") |
No edit summary |
||
| Line 1: | Line 1: | ||
[[Image:shape.png|thumb|right|The shape of superballs interpolates between octahedra (''q'' = 0.5) and cubes (''q'' = ∞) via spheres (''q'' = 1).]] | [[Image:shape.png|thumb|right|The shape of superballs interpolates between octahedra (''q'' = 0.5) and cubes (''q'' = ∞) via spheres (''q'' = 1).]] | ||
A superball is defined by the inequality | |||
:<math>\frac{x^2}{a^{2q}} + \frac{y^2}{a^{2q}} + \frac{z^2}{a^{2q}} \le 1</math> | |||
where ''x'', ''y'' and ''z'' are scaled Cartesian coordinates with ''q'' the deformation parameter, and we use radius a of the particle as our unit of length. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (''q'' = 0.5) and the cube (''q'' = ∞) via the sphere (''q'' = 1) as shown in the left figure. | |||
Revision as of 19:57, 16 September 2012
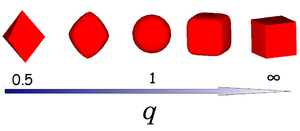
A superball is defined by the inequality
where x, y and z are scaled Cartesian coordinates with q the deformation parameter, and we use radius a of the particle as our unit of length. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (q = 0.5) and the cube (q = ∞) via the sphere (q = 1) as shown in the left figure.
