Hard superball model: Difference between revisions
Jump to navigation
Jump to search
Carl McBride (talk | contribs) m (Added Category (Models)) |
Carl McBride (talk | contribs) m (Added some internal links) |
||
| Line 2: | Line 2: | ||
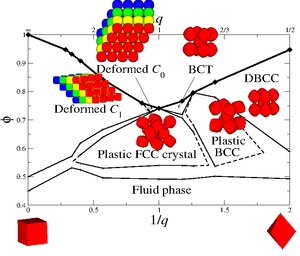
[[Image:phase_diagram_superball.png|thumb|right|Phase diagram for hard superballs in the <math>\phi</math> (packing fraction) versus 1/''q'' (bottom axis) and ''q'' (top axis) representation where ''q'' is the deformation parameter [2].]] | [[Image:phase_diagram_superball.png|thumb|right|Phase diagram for hard superballs in the <math>\phi</math> (packing fraction) versus 1/''q'' (bottom axis) and ''q'' (top axis) representation where ''q'' is the deformation parameter [2].]] | ||
The '''hard superball model''' is defined by the inequality | |||
:<math>\left|\frac{x}{a}\right|^{2q} + \left|\frac{y}{a}\right|^{2q} +\left|\frac{z}{a}\right|^{2q} \le 1</math> | :<math>\left|\frac{x}{a}\right|^{2q} + \left|\frac{y}{a}\right|^{2q} +\left|\frac{z}{a}\right|^{2q} \le 1</math> | ||
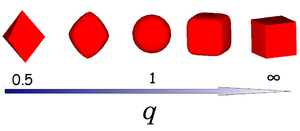
where ''x'', ''y'' and ''z'' are scaled Cartesian coordinates with ''q'' the deformation parameter and radius ''a''. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (''q'' = 0.5) and the cube (''q'' = ∞) via the sphere (''q'' = 1) as shown in the left figure. | where ''x'', ''y'' and ''z'' are scaled Cartesian coordinates with ''q'' the deformation parameter and radius ''a''. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (''q'' = 0.5) and the [[Hard cube model |cube]] (''q'' = ∞) via the [[Hard sphere model |sphere]] (''q'' = 1) as shown in the left figure. | ||
== Particle Volume == | == Particle Volume == | ||
| Line 17: | Line 17: | ||
\end{eqnarray} | \end{eqnarray} | ||
</math> | </math> | ||
where <math>\Gamma</math> is the Gamma function. | where <math>\Gamma</math> is the [[Gamma function]]. | ||
==Overlap algorithm== | ==Overlap algorithm== | ||
The most widely used overlap algorithm is on the basis of Perram and Wertheim method<ref>[http://dx.doi.org/10.1016/0021-9991(85)90171-8 John W. Perram and M. S. Wertheim "Statistical mechanics of hard ellipsoids. I. Overlap algorithm and the contact function", Journal of Computational Physics '''58''' pp. 409-416 (1985)]</ref> <ref>[http://dx.doi.org/10.1039/C2SM25813G R. Ni, A.P. Gantapara, J. de Graaf, R. van Roij, and M. Dijkstra "Phase diagram of colloidal hard superballs: from cubes via spheres to octahedra", Soft Matter '''8''' pp. 8826-8834 (2012)]</ref>. | The most widely used overlap algorithm is on the basis of Perram and Wertheim method <ref>[http://dx.doi.org/10.1016/0021-9991(85)90171-8 John W. Perram and M. S. Wertheim "Statistical mechanics of hard ellipsoids. I. Overlap algorithm and the contact function", Journal of Computational Physics '''58''' pp. 409-416 (1985)]</ref> <ref name="superballs">[http://dx.doi.org/10.1039/C2SM25813G R. Ni, A.P. Gantapara, J. de Graaf, R. van Roij, and M. Dijkstra "Phase diagram of colloidal hard superballs: from cubes via spheres to octahedra", Soft Matter '''8''' pp. 8826-8834 (2012)]</ref>. | ||
==Phase diagram== | ==Phase diagram== | ||
The full phase diagram of hard superballs whose shape interpolates from cubes to octahedra was reported in Ref | The full [[phase diagrams |phase diagram]] of hard superballs whose shape interpolates from cubes to octahedra was reported in Ref <ref name="superballs"> </ref>. | ||
==References== | ==References== | ||
Revision as of 10:16, 18 September 2012
The hard superball model is defined by the inequality
where x, y and z are scaled Cartesian coordinates with q the deformation parameter and radius a. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (q = 0.5) and the cube (q = ∞) via the sphere (q = 1) as shown in the left figure.
Particle Volume
The volume of a superball with the shape parameter q and radius a is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{eqnarray} v(q,a) & = & 8 a^3 \int_{0}^1 \int_{0}^{(1-x^{2q})^{1/2q}} (1-x^{2q}-y^{2q})^{1/2q} \mathrm{d}\, y \, \mathrm{d}\, x \nonumber\\ & = & \frac{8a^3\left[ \Gamma\left(1+1/2q\right) \right]^3}{\Gamma\left(1+ 3/2q\right)}, \end{eqnarray} }
where is the Gamma function.
Overlap algorithm
The most widely used overlap algorithm is on the basis of Perram and Wertheim method [1] [2].
Phase diagram
The full phase diagram of hard superballs whose shape interpolates from cubes to octahedra was reported in Ref [2].
References
- ↑ John W. Perram and M. S. Wertheim "Statistical mechanics of hard ellipsoids. I. Overlap algorithm and the contact function", Journal of Computational Physics 58 pp. 409-416 (1985)
- ↑ 2.0 2.1 R. Ni, A.P. Gantapara, J. de Graaf, R. van Roij, and M. Dijkstra "Phase diagram of colloidal hard superballs: from cubes via spheres to octahedra", Soft Matter 8 pp. 8826-8834 (2012)