Hard superball model: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 5: | Line 5: | ||
:<math>\left|\frac{x}{a}\right|^{2q} + \left|\frac{y}{a}\right|^{2q} +\left|\frac{z}{a}\right|^{2q} \le 1</math> | :<math>\left|\frac{x}{a}\right|^{2q} + \left|\frac{y}{a}\right|^{2q} +\left|\frac{z}{a}\right|^{2q} \le 1</math> | ||
where ''x'', ''y'' and ''z'' are scaled Cartesian coordinates with ''q'' the deformation parameter | where ''x'', ''y'' and ''z'' are scaled Cartesian coordinates with ''q'' the deformation parameter and radius ''a''. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (''q'' = 0.5) and the cube (''q'' = ∞) via the sphere (''q'' = 1) as shown in the left figure. | ||
Revision as of 19:59, 16 September 2012
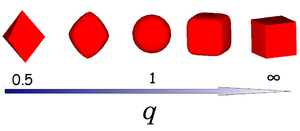
A superball is defined by the inequality
where x, y and z are scaled Cartesian coordinates with q the deformation parameter and radius a. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (q = 0.5) and the cube (q = ∞) via the sphere (q = 1) as shown in the left figure.
