Hard superball model: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
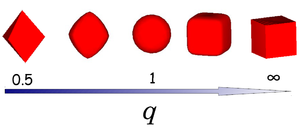
[[Image:shape.png|thumb|right|The shape of superballs interpolates between octahedra (''q'' = 0.5) and cubes (''q'' = ∞) via spheres (''q'' = 1).]] | [[Image:shape.png|thumb|right|The shape of superballs interpolates between octahedra (''q'' = 0.5) and cubes (''q'' = ∞) via spheres (''q'' = 1).]] | ||
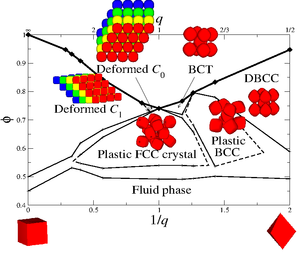
[[Image:phase_diagram_superball.png|thumb|right|Phase diagram for hard superballs in the <math>\phi</math> (packing fraction) versus 1/''q'' (bottom axis) and q (top axis) representation where ''q'' is the deformation parameter [2].]] | [[Image:phase_diagram_superball.png|thumb|right|Phase diagram for hard superballs in the <math>\phi</math> (packing fraction) versus 1/''q'' (bottom axis) and ''q'' (top axis) representation where ''q'' is the deformation parameter [2].]] | ||
A superball is defined by the inequality | A superball is defined by the inequality | ||
Revision as of 21:08, 16 September 2012
A superball is defined by the inequality
where x, y and z are scaled Cartesian coordinates with q the deformation parameter and radius a. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (q = 0.5) and the cube (q = ∞) via the sphere (q = 1) as shown in the left figure.
Particle Volume
The volume of a superball with the shape parameter q and radius a is given by
- Failed to parse (unknown function "\begin{eqnarray}"): {\displaystyle \begin{eqnarray} v(q,a) & = & 8 a^3 \int_{0}^1 \int_{0}^{(1-x^{2q})^{1/2q}} (1-x^{2q}-y^{2q})^{1/2q} \mathrm{d}\, y \, \mathrm{d}\, x \nonumber\\ & = & \frac{8a^3\left[ \Gamma\left(1+1/2q\right) \right]^3}{\Gamma\left(1+ 3/2q\right)}, \end{eqnarray} }
where is the Gamma function.
Overlap algorithm
The most widely used overlap algorithm is on the basis of Perram and Wertheim method[1] [2].
Phase diagram
The full phase diagram of hard superballs whose shape interpolates from cubes to octahedra was in Ref.[2].
References
- ↑ John W. Perram and M. S. Wertheim "Statistical mechanics of hard ellipsoids. I. Overlap algorithm and the contact function", Journal of Computational Physics 58 pp. 409-416 (1985)
- ↑ R. Ni, A.P. Gantapara, J. de Graaf, R. van Roij, and M. Dijkstra "Phase diagram of colloidal hard superballs: from cubes via spheres to octahedra", Soft Matter 8 pp. 8826-8834 (2012)


