Hard superball model

The shape of superballs interpolates between octahedra (q = 0.5) and cubes (q = ∞) via spheres (q = 1).

Phase diagram for hard superballs in the $\phi$ (packing fraction) versus 1/q (bottom axis) and q (top axis) representation where q is the deformation parameter [2].

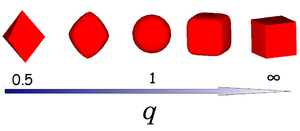
A superball is defined by the inequality

$\left|{\frac {x}{a}}\right|^{2q}+\left|{\frac {y}{a}}\right|^{2q}+\left|{\frac {z}{a}}\right|^{2q}\leq 1$

where x, y and z are scaled Cartesian coordinates with q the deformation parameter and radius a. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (q = 0.5) and the cube (q = ∞) via the sphere (q = 1) as shown in the left figure.

Particle Volume

The volume of a superball with the shape parameter q and radius a is given by

Failed to parse (unknown function "\begin{eqnarray}"): {\displaystyle \begin{eqnarray} v(q,a) & = & 8 a^3 \int_{0}^1 \int_{0}^{(1-x^{2q})^{1/2q}} (1-x^{2q}-y^{2q})^{1/2q} \mathrm{d}\, y \, \mathrm{d}\, x \nonumber\\ & = & \frac{8a^3\left[ \Gamma\left(1+1/2q\right) \right]^3}{\Gamma\left(1+ 3/2q\right)}, \end{eqnarray} }

where $\Gamma$ is the Gamma function.

Overlap algorithm

The most widely used overlap algorithm is on the basis of Perram and Wertheim method .

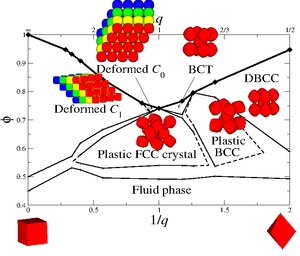
Phase diagram

The full phase diagram of hard superballs whose shape interpolates from cubes to octahedra was in Ref.[2].